知っておくといいだろうなって程度の話。
僕らは現在、ほぼ平均律のみで音楽的コミュニケイションを行う習慣の中に居る。
ところが実は純正律 的 やりとりも普通に行われている。
それを解っておくと演奏上の悩みを、考えたり・解決したり・妥協したり、って時の心の支えになるんじゃないかなってことです。
そんな知識の整理を書き付けます。
※ 読み返してみたら、重大な書き間違えや、あまりに不親切やら、解りにくい!やら色々気になったので訂正加筆をしました。今後も随時わかり易くしてくつもりですm(_ _)m _20221226
平均律も純正律も調律法の一種
平均律とは、
1オクターブの間を周波数の比率として12等分した1つを半音として、その半音の間隔で音高を上に向かって並べると最初の音(基音)から13個目で1オクターブ上に到達するようにしたもの。
純正律とは、
倍音列に内在する音程関係を巧く使った調律法。
Ⅰの和音・Ⅳの和音・Ⅴの和音、その3つだけは調和的に響くように工夫されてます。
Ⅰの和音はドミソ、Ⅳはファラド、Ⅴはソシレ、
それらは主要三和音と呼ばれてますね。
Cメイジャーで例示すると…
純正律では、ドを基音とする倍音列の中にミとソを見つけ、
そのソを基音とする倍音列の中にシとレを見つけ、
ドからまたファを見つけ、それを基にラを見つけます。
そこまでで、ドレミファソラシの7音が登場するが、
それ以外の5つの音(=臨時記号の要る音)の決め方は様々に有り得る。
純正律の残念な点、
主要三和音以外の三和音(団子三兄弟の形にした和音)は調和的には響かない。
つまり、転調すると気味悪い音になりやすい。
(後でまた詳しく説明しますね)
それらを解決するために幾つもの純正的な調律法が考え出されました。
J.S.バッハさんは転調を自由にしたかった人なので、調律法には殊更に興味が深かったのでしょう。
日本語では「平均律クラヴィア曲集」と呼ばれる曲がありますが、原題を英語で言えば「well tenpered」つまり「上手に調律された」です。
その当時使われた調律は「ミーントーン=中全音律」と呼ばれるもので純正律の改良型の1つ。
不均等型平均律と言えなくもないが、完全なる転調の自由があったとは言い難い。
そのジレンマを、響きの調和については妥協しつつも解決した方法が平均律と言えます。
平均律はユニゾンとオクターブ以外どこをとってもハモらない。
その代わり、どのキーに転調しても大丈夫。
※参考、クラヴィア曲集について
http://pietro.music.coocan.jp/storia/bach_bentemperato1_2.html
と
http://www.music.qub.ac.uk/tomita/essay/wtc1j.html
調律楽器・調音楽器・噪音楽器
「調律」とは、鍵盤楽器や鍵盤打楽器などで鳴らせる各音高を、西洋音楽を扱えるような高さに調整することです。
つまり、演奏中に臨機応変に音高調整をできないタイプの楽器に必要な作業とその結果のこと。
そういった「調律の必要な楽器」のことを「調律楽器」と呼びます。
あまたある楽器の多くは臨機応変に音高の微調整ができます。
それらを「調音楽器」と呼びます。
フレットの無い弦楽器であるヴァイオリンや、スライドで音高を作るトロンボーンなど思い浮かべると解り易いですね。
見た目は調律的に見えるかもしれない「運指」を伴う管楽器も、実は全て調音楽器です。
なぜならば、演奏者が調音操作をしないかぎり必ず音痴になりますから。
ヴォーカルもその一つです。
フレットのついた弦楽器は中間的な楽器群と言えるでしょう。
チョーキングあるいは「強く掴」めば音高を上ずらせられます。
棹をグイっと撓ませればブラ下げられます。
とはいえ、管楽器のような調音楽器群よりは若干不自由と言えるし、普通に演奏する限りは、調律した結果の音を「頑張らずとも」確定的に発音できます。なので中間的なわけです。
ちなみに音高を明瞭に聴き分けられないタイプの打楽器などには、この捉え分けの概念は、そのままには適用されません。
はっきりと音高を呼び分けられるわけではないですから。
「楽音と噪音」という言葉があります。
楽音は、音高を明瞭に聴き分けられる音。
噪音は、音高を明瞭に聴き分けられない音。
楽音は、基本的な振動数に対して、付随して発生する諸振動(=上音)が、割と綺麗に整数倍の振動数として並んでいます。
そうすると音高を聞き分け易くなります。
噪音は、上音の周波数に、整数倍でないものを含む割合が高い音と言えます。
その場合、基本周波数の音高すら明瞭に聞き分けにくくなります。
そんなわけで、
楽音を出す楽器を楽音楽器、
噪音を出す楽器を噪音楽器 と呼びます。
つまり、音高を聞き分けにくい打楽器などは噪音楽器の一種と言えます。
!!「騒音」じゃありませんからねっ!!
とはいえ、そういった打楽器でも
「どっちかといえば高いとか低いとか」は言えます。
聞き分けにくいとは言え、基本振動数はあるし、含まれる上音の傾向によっても印象づけられます。
なので「打楽器なりの調律」という捉え方はできます。
「ドラムセットのチューニング」といった言葉はそれを表しますね。
ですが、本稿で扱う平均律・純正律という概念の世界とは別の所にある楽器群とは言えます。
そうそう、ティンパニーだけは特別ですね。
明瞭に音高を聞かせてくれるし、音高を連続的に調整できる楽器なので調音楽器と呼べます。
地球は広いので、楽器は西洋楽器ばかりではありません。
沢山の民俗楽器も観察して、どれが調律楽器?調音楽器?噪音楽器?と観察してみましょう。
自然倍音列とは…
音階・調律を理解する基礎になるので簡単に整理しますね。
物体が持続的(カンマ数秒でも)振動を起こし、それが空気に疎密波を生み、それが周期的圧力として鼓膜に伝わった時に音として感知される。
自然界の音(つまり人工的にのみ発生しうる純音=基本振動数のみの音、でない限り)は基本振動数のみならず、それよりも高い周波数の音を多様に含む。
それらを「上音」と呼びます。
人に「ある高さの音」として認識されやすい場合、その音には「自然倍音」が内在されてます。それは基本周波数の、ほぼ整数倍の上音のこと。
つまり、自然倍音、略して倍音は上音の一種で、倍音が多く含まれれば音高を認識しやすいってわけ。
音高を認識しやすい音を「楽音」と呼びます。
音楽に使うに相応しい音だからです。
「楽音である」と言える条件2つ
・基本的振動がほぼ一定の振動数で安定してること。
・内在する上音群が整数倍である傾向が強いこと。
その「整数倍の上音群」のことを「自然倍音、略して倍音」と呼ぶわけですね。
基本的振動数を第1次倍音=基音、
2倍の周波数の上音を第2次倍音、
3倍の、、、
と呼び分けます。
それら倍音群の行列を「自然倍音列、略して倍音列」と呼びます。
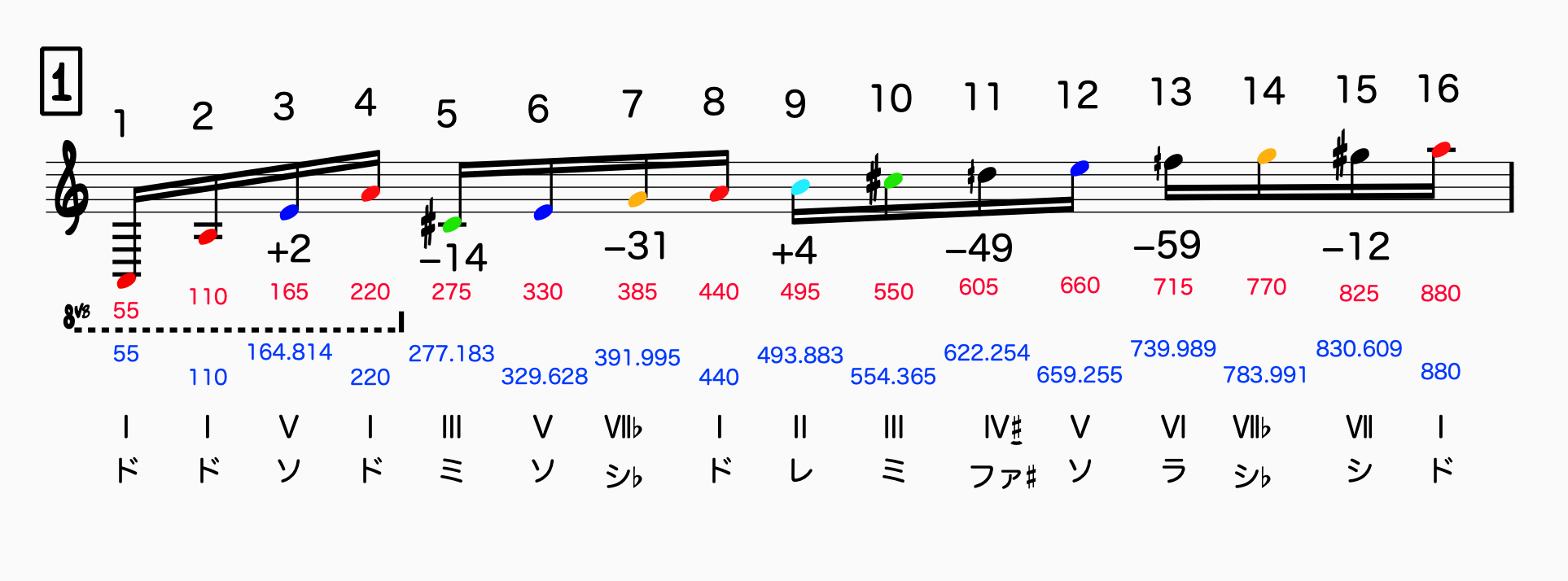
↑譜表上の数字は「第○次倍音」を示します
音符すぐ下の黒数字は、平均律からのズレをセントで示します。
赤数字は自然倍音の周波数
青数字は参考として平均律の周波数
その下の黒文字は、Aをトニックとした音度と移動ド唱法式の階名
基音を仮に 55Hz とします。
「Hz」とは振動が「1秒間に何往復するか」を表す単位です。
第2次倍音は 110Hz となります。
基音の2倍。基音との周波数比率は1:2(第○次倍音の数字と一致します)。
音楽的に聞こえ方を言い表すなら「基音の1オクターブ上」と聞こえます。
第3次倍音は 165Hz。
基音の3倍、第2次倍音の 3/2倍。
基音とは1:3、第2次とは 2:3の比率。
基音から1オクターブと完全5度上に聞こえます。
基音を仮に「ド」と呼ぶとしたら「ソ」と聞こえます。
第4次倍音は 220Hz。
基音の4倍、第2次の 2/4 つまり2倍、
第3次倍音の 4/3 倍。
基音とは1:4、第2次とは2:4、
第3次とは3:4の比率。
基音から2オクターブ上の「ド」。
第5次倍音は 275Hz。
基音の5倍。2次の 5/2倍、
3次の 5/3倍、4次の 5/4倍。
基音とは1:5、2次とは2:5
3次とは3:5、4次とは4:5。
基音から2オクターブと長3度上の「ミ」。
第6次倍音は 330Hz。
基音の6倍。2次の 6/2 つまり3倍、
3次の 6/2 つまり2倍、
4次の 6/4 つまり 3/2 倍
5次の 6/5 倍。
基音とは1:6、2次とは2:6=1:3
3次とは3:6=1:2
4次とは4:6=2:3
5次とは5:6
基音から2オクターブと完全5度上の「ソ」
第7次倍音は 385Hz。
基音の7倍、2次の7/2倍、
3次の7/3倍、4次の7/4倍、
5次の7/5倍、6次の7/6倍。
基音とは1:7、2次とは2:7、
3次とは3:7、4次とは4:7
5次とは5:7、6次とは6:7
基音から2オクターブと短7度上の「シ♭」
第8次倍音は 440Hz。
基音の、、、
、、、あとは御自分で書けますね (^_^;
興味ある方は是非続けてください。
ちなみに平均律と比べると、
ソは2セント高く(小数点以下四捨五入)
ミは 14セント低く、
シ♭は 31セント低い(純正律の −12セントとは一致しません)、
ラは猛烈に低い(笑
のも覚えておくとよいでしょう。
「セント」とは、平均律での半音を100等分した音程のことです。
つまり、平均律での半音は100セント、全音は200セント、1オクターブは1200セントという距離として表されます。
音名と階名
さきほどの倍音列表。
A音を「仮にドと呼んで…」という方式に、
表を目で見た途端に混乱しはじめた方も多いかと。
五線譜の上で A音を見ると「ドレミで言えばラ」
「ラとしか呼べない」
という方式で、音の高さの呼び名を扱う人が多いからです。
上でディグリーの説明をしましたね。
ローマ数字とアラビア数字の使い分け。
使い分けるには理由があるんです。
それぞれの存在理由が。
ってことは同様に…
ABC での呼び名、
ドレミでの呼び名、
なぜ2つの方式があるのかな?
それぞれの存在理由があるはずですよね?
ABC はドイツ語英語で、ドレミはイタリア語
なんて説明を見かけることがあるが、それはインチキと思ってよいです。
世界の言葉はもっと沢山あるし、ドレミもABCももっと色んなとこで使われてるんだから全部列挙してくんなきゃね。
ってぇのは半ば冗談として、、
言語による違いを並べるのなら他に幾つも呼び名スタイルはあるので、教科書的なものに↑のような説明はあまりに情けないです。
ちゃんとした説明は↓に書いたので御参照くださいませ。
倍音が音階と和声の起源
空間に1つ楽音が鳴れば、そこから幾つもの音高が、
「聞き分けられる」ということです。
普通それは「1つの音」として聞こえるので、各倍音の音高を聞き分けるのは難しい。
ですが、
耳を研ぎ澄ます方法はあり、聞き分けられるようになります。
簡単に聞き分ける方法もあります。
楽器での倍音奏法です。
管弦楽器でハーモニクスやフラジオレットと呼ばれる奏法ですね。
弦長・管長を変えずにそれをした場合に登場する幾つかの音、それが倍音です。
聞き分けられた複数の音高群。
それこそが「音階の起源」の1つと言えます。
同時に和声=ハーモニーの起源とも言えます。
倍音列の中に登場する音程(音高間の距離)で2つの音を鳴らすと、まるで1つの音の様に調和し、一体化するだけでなく、共鳴(響き合い)の効果で、
その空間に、まるでパイプオルガンでその倍音群をドカンと弾いたような現象を起こします。
それが「ハモり」です。
人類はそれを少なからず快く感じるので、
それを再現をすべく試行錯誤するわけですね。
その結果が音楽的概念としてのハーモニー=和声なのだと筆者は理解しています。
人類史上でその試行錯誤が起きた瞬間に、倍音という物理現象は、ハーモニーという音楽の行いに変質したのだと思います。
ちなみに、
倍音を聞き分けられるようにしたり、ハモりを巧い具合に作れるようにってなトレーニング法を色々と提案したのが↓です。
『大人が始めるソルフェージュ_大人ソルフェシリーズ2基礎技術編』
http://bit.ly/KT_otona-solfege
協和と不協和、完全音程・不完全協和音程・不協和音程
その調和・共鳴の「程度」は、倍音列に早いうちに登場する音程ほど強いです。
後の方に登場する音程になると効果は薄くなっていきます。
さきほど書いたパイプオルガン現象は、同時に鳴らす2音の音程が、倍音列に早く登場するものと一致するほど強く現象します。
それは「協和~不協和」という概念と一致します。
倍音列もどんどん辿っていけば、登場する音程関係はどんどん狭くなり、
長2度(=全音)や短2度(=半音)に相当する音程も登場し、
更に狭い音程も出て来ます。
狭い音程は上手にハモるのが難しいですよね。
ハモってるか否かの掴み所が希薄です。
そういった狭い音程のことを不協和的と呼ぶわけです。
逆に、
倍音列に早い内に登場する音程は協和的。
すなわち、うまくハモったか否かを判断しやすい。
ハモれてればパイプオルガンがドカンと鳴りますから。
協和と不協和の間に明確な境界線はありません。
ですが、
第4次倍音までは「誰にも確定的に=迷わずに高さを聞き取れる」音程で、かつ、
同時に鳴らすとまるで1つの音のように完全に調和します。
なので特にそれらを「完全協和音程」と呼び分けます。
・完全1度_ユニゾン
・完全8度_オクターブ
・完全5度
・完全4度
そこから第6次倍音までに登場する音程は、割と明瞭に特定できるし、
ハモり(=基の倍音列を想起させる響き)も快く響く。
それらの音程を「不完全協和音程」と呼びます。
・長3度・短3度
・短6度・長6度
それより高次の倍音域になると、長3度・短3度・長2度・短2度などが、
微細音程の変化として沢山のバラエティが登場します。
つまり、ある音程を確定的に定められなくなります。
その領域に登場する音程、そのうち、
第6次までに特定される「長3度、短3度」ではない長2度より狭い音程を「不協和音程」。
・長2度・短2度
・短7度・長7度
翻って言えば、その領域に長3度・短3度も沢山のバリエイションが見つかります。
それが「不完全」と呼ぶ所以とも言えますね。
ともあれ、そんな風に呼び分けられてます。
つまり、上手にハモろうとするなら、
倍音列の早い内に登場する音程ほど「判断基準を掴みやすい」、
遅くに登場する音程にはバリエイションがありパチっと決めにくい、ということです。
とはいえ、
難しいながらも、半音にさえハモるツボはあるわけです。
純正律とは
純正律とは、第5倍音までに登場する音程のみを利用した音律です。
「Ⅰから、Ⅳから、Ⅴから」の3つの倍音列それぞれの第5倍音までの音、
を組み合わせると7音から成る長音階がうまく作れるし、
Ⅰの和音、Ⅳの和音、Ⅴの和音、それぞれは 美しく協和します。
Ⅰの音群を基準とすると、Ⅳの音群は2セント低く、Ⅴの音群は2セント高くします。
それで、ⅠとⅣ、ⅠとⅤ の関係は調和しやすくなるが、
ⅣとⅤの各音群間には矛盾 = 高い不協和が生まれます。
その矛盾を解決しようとしたのが音律=調律法の歴史です。
純正律では、3つの倍音列をクルクルと乗り換えながら和声進行を進めます。
それが「機能和声法」の確立に貢献したとも言えるでしょう。
トニック_Ⅰの倍音列に含まれる音群_Ⅰとドと呼ぶならドミソ。
サブドミナント_Ⅳの倍音列に含…_ファラド
ドミナント_Ⅴの倍音列に含…_ソシレ
つまり純正律では「ラ」が鳴ってればその間は、サブドミナント音群のピッチに支配されます。
「シ」が鳴ってればドミナント音群のピッチに、「ミ」が鳴ってればトニックに。
つまり純正律とは、
「3つの倍音列の基音=3つのトニック=3つのキーの主音」
を行き来するのが当たり前、が前提の音律(=調律法)です。
「倍音の基音を乗り換える」=「転調」
とも言えます。
機能和声の成立を喚起したとも言える調律法ですが矛盾もはらみます。
機能和声は、ドミナント、サブドミナントともにトニックへの解決欲求を感じさせる必要がありますが、各倍音列にシフトすると、それぞれ調和=安定した響きとなり、トニックへの引力は弱まります。
そんなとこが純正律のあらましです。
(実はこの項目、↓に書いた一部からの引用↓も見ると面白いかも…)
純正律の成り立ち
純正律とは、ある高さの音(基音)を鳴らせば自然倍音列が認識され、その中で
「誰にも確定的に捉えられる音程」
つまり完全8度・完全5度・完全4度と
「わりと確定的な音程」つまり長3度・短3度
とを使って、
・主和音(Ⅰの和音、移動ド的に言えばドミソ、ディグリーで言えば135)
・下属和音(Ⅳの和音、ファラド、461)
・属和音(Ⅴの和音、ソシレ、571)
の3つの和音だけは調和的に響くように調律したもの。
※「ディグリー」
長音階に主音から順に1234567と番号付けして呼ぶ方法。
厳密にはローマ数字とアラビア数字とで使い分けられます。
・ローマ数字_あるトーナルセンター=調的中心(気楽には主音と言う)に支配されている間、その主音をⅠとし、そこから長音階に沿ってⅠⅡⅢ Ⅳ Ⅴ Ⅵ Ⅶ と呼ぶ。
・アラビア数字_転調(=トーナルセンターの変更)が無くとも、便宜的に本来の基音ではない音高を1とすると便利な時に使う。一時転調を扱ったり、コードに対してのアヴェイラブルノートスケールを表示したり、和声の「その時点での」構造を説明したりする時に。
(トーナルセンターとは…については近いうちに書きますね)
はい、話を戻します。
先ずは基音=トーナルセンターとしてある音高を規定する。
その倍音列から、
・基音の完全5度上(第3倍音、ソ、Ⅴ)と
・長3度上(第5倍音、ミ、Ⅲ)
は確定的な「高さ」として聴き分けられる。
それを使って Ⅰ の和音は全く調和的な和音として確定されます。
譜例では便宜的に「ド」を「C音」として例示しますね。
「全く調和的な」とは、
「ある倍音列に含まれる諸音高と一致する」
すなわち、
「まるで1つの音のように聞こえる」
ということです。
平均律と比べると、ソは2セント高く、ミは14セント低くなります。
さて、
完全5度上の音、ソ・Ⅴ、を新たな基音として、
その完全5度上の音高を求められます。
それは、最初の基音ド・Ⅰから見ればレ・Ⅱとなります。
新たな基音ソ・Ⅴから見てその長3度上も確定的に求められます。
それは、最初の基音ド・Ⅰから見ればシ・Ⅶ となります。
この決め方をするとソは平均律より2セント高いから、
レは4セント高く、シは12セント低くなります。
次に、
最初の基音ド・Ⅰから完全5度下の音高ファ・Ⅳも確定的に求められます。
ファ・Ⅳを、また新たな基音と想定して、その第3倍音がド・Ⅰ であるようなファの高さを逆算的に導くわけです。
その結果の音高が、ド・Ⅰ の完全5度下のファ・Ⅳとして確定されます。
そのファ・Ⅳを新たな基音として、ラ・Ⅵも導き出されますね。
この場合、ファは2セント低く、ラは16セント低くなります。
ここまでで、ドレミファソラシは勢揃いします。
さて、
そこで見つかった音高を使って「レファラ」という和音を鳴らすとします。
レとラは完全5度(つまり平均律の完全5度より2セント広い)であって欲しいところですが、
レが4セント高く、ラが16セント低いので、その完全5度は平均律より20セント狭くなり、全く調和しません。
さらに、
レが4セント高く、ファが2セント低いので、
純正短3度は平均律よりも16セント広いはずですが、
6セント狭い、つまり在るべき広さよりも 22セントも狭い。
ついでに、、
ファが2セント低く、ラが16セント低いので、
平均律より14セント狭いはずの所が、、
あ!ここだけはバッチリですね。
ともあれ、レファラは濁ります。
結果的に、
・主要三和音以外の和音は使いにくい
・転調に対しては不自由
そんな調律法と言えます。
先述の通り、臨時記号のつく音についても、悪く言えば不確か、よく言えば融通の効く音高を選ぶことになります。
それも転調の結果の不味さに繋がります。
とはいえ、
「調による色合いの違い」
を佳い特徴として作曲に利用するのは有り得たようで、
今の平均律の世の中より、調による色調の違いを味わう楽しみはあったようですね。
!! なのですけどね !!
調音楽器では レファラ も美しく響かせられます。
なぜならば、レ~ラを純正完全5度にするような調整を臨機応変にできるからです。
なので、
上記の不自由は調律楽器ならではのものです。
平均律とは
1オクターブの音程を数理的に 12等分する調律法。
純正で(倍音列に出てくるのと同じで)美しく調和した和音は鳴らせないが割と近似ではある。
かわりに、どのキーに転調しても均質なのがメリット。
平均律の成り立ち
ざっくり書きますよ。
その昔ピタゴラスさんは純正律とは別の方法でオクターブを丁度よく満たす音階、それを構成する音程群を規定しようとしました。
基準として基音と第3次倍音に着目。
誰もが迷わずに、ある1音の倍音列から聴き取れる音程だから。
基音を仮にドと呼びます。
第3次倍音に当たる音は完全5度上のソに相当します。
ソの音を新たな基音として、その第3次倍音はレにあたる音です。
レからラ、ラからミ、ミからシ、シからファ♯、
ファ♯をソ♭と読み替えてそこからレ♭、
レ♭からラ♭、ラ♭からミ♭、ミ♭からシ♭、シ♭からファ、
そして、ファからド、
と、最初のドに辿り着いて\(^O^)/これで12の半音が見つかった!
ギリシャの4弦の竪琴の代表的調律法ディアトノンを色んな高さに変えてもうまくマネージメントできそう!
と思いきや、最初のドと少しズレちゃうのです。
のちの時代の言い方だと 24セント高いんです。
お察しの通り、
純正完全5度は平均律より2セント広い、それを12回重ねるわけだから、2×12=24 。
これはなんとかツジツマを合わせたい。
純正律側での四苦八苦とも組んず解れつで、ベストな調律法を探す歴史は始まったわけですね。
で、だいぶ時が経ってから数学の発展にも助けられて、
ハイ、ガッチャンコって感じに平均律が登場しました。
平均律は純正律から発展した数々の調律法と比べると、自然倍音に依拠した調和的音程を尊重する所は皆無なのが違う所ですね。
とにかく等分に、って点では、どちらかといえばピタゴラス的発想に近いとは言えなくも無い。
この生まれ育ちは↓でもう少し詳しく書きました。
ちなみに、
完全5度上の見つけ出しを12回すると、少しズレた最初の音に辿り着くが、それは「別の音」として、そのまま繰り返しを続ける、というトライも行われました。
で、最初の音と同じ音に辿り着くわけですが、そこまでに大変な回数となります。
ですが、それを鍵盤に置き換えて楽器を作ってみる人達も居たわけです。膨大な鍵盤数にはなかなか圧倒されます。
そこで聞けるのは半音よりも狭い音程達です。
それらをもって、中近東で普通に演奏に用いられる「微分音」の根拠として説明や研究をする人も居てなかなか面白いです。
平均律は転調の自由ばかりでなく…
鍵盤楽器産業の都合でもあったのでしょう。
商品化と大量生産を目指すには規格化が必要でしょうから。
ちなみに 標準ピッチ の歴史的変遷にも同じことが言えますね。
興味のある方はググってみましょう。
ともあれ平均律は僕らに、どこに転調しても均質な響きを与えてくれました。
それと同時に調律楽器では、自然にかなった調和した響きは失われたわけです。
ですが幸いなことに、人間の耳は積極的ファジーにできてるようで。
ちょっとした誤差なら「きっとこういうことだろう」と前向きに解釈して、美しく聴き取るという能力も備わってるようです。
気の持ちようとも言えるでしょうが。
ですが、響きの調和・不調和を聞き分ける能力が劣化したのは否めないでしょう。
転調自由な純正律? 調音楽器の日常
調音楽器の世界は今でも純正的やりとりが多いです。
よいハーモニーを作るには純正的な(=倍音列に適った音程関係による)音程を目指して、音高調整をする必要があるからです。
調律楽器での純正律では転調の自由がありませんでしたが、調音楽器なら臨機応変に音高を変えられるので、いつどの調に行っても対応できます。
つまり、転調自由な純正律(的かつ流動的な)音律を扱えるということです。
それ以前に、
主要三和音以外の和音でも純正的=ハモる和声を実現できます。
「今、どのキーに居るのか」
つまり、
「どの基音によって立つ倍音列の中に居るべきなのか」
を解っていれば、適確な音高調整を目指せます。
あるキーの中に居たままだとしても、主要三和音以外の和音(三和音に限らず)では、必要となる調整をすることにもなります。
そういった扱いをできるようにするために、音楽理論の勉強も役に立ちます。
もちろん、ソルフェージュの訓練も大切です。
なのですが、、、
平均律な調律楽器との合奏でのジレンマ
調音楽器だけでの合奏ならば自由に音高調整をして、その時々での調和を作れます。
ところが殆どの合奏体では調律楽器も同居します。
すると、調律楽器は絶対的頑固に平均律を貫くので、
それとはどう付き合うか、が課題となります。
その点は充分に面白い話となるので、稿を改めてゆっくり書きますね。
それ以前の知識の整理としてはここまでにしておきます。
ではまた(^^)/
コメント